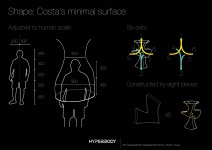
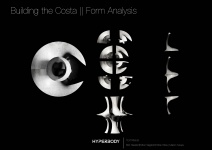
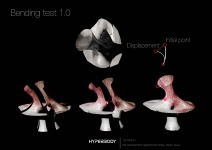
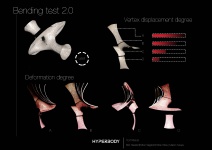
The main appearance of the structure is based on the mathematical embedded minimal surface discovered in 1982 by Celso José da Costa. The topology is created by puncturing a compact surface, therefore becoming a finite topology. The current design is a topologically thrice-punctured torus which is deformed until the planer end becomes catenoidal. The topology can be described using the Weierstrass zeta and the Weierstrass elliptic functions.